Symmetric-key cryptography

As mentioned in the previous post previous post in the Symmetric-key cryptosystems, both the sender and receiver use the same key - a secret key.

The picture shows plaintext is encrypted into ciphertext on the sender side and the same key (key copy) is used to decrypt the ciphertext to plaintext. As long as both sender and recipient know the secret key, they can encrypt and decrypt all messages that use this key.

This requirement, that both parties must know the same secret key is one of the main drawbacks of symmetric key encryption, in comparison to public-key encryption. However, there are also good reasons why symmetric keys are used widely.

We already know about ciphers and two basic groups of symmetric ciphers. I’m going to cover both details below

Stream ciphers

In-stream cipher plaintext digits are combined with a pseudorandom cipher digit keystream. Each plaintext digit is encrypted one at a time with the corresponding digit of the keystream, to give a digit of the ciphertext stream.

OTP as model

The the one-time pad (OTP) is an encryption technique that cannot be cracked if used correctly since it’s been proven that any cipher with the perfect secrecy¹ property must use keys with effectively the same requirements as OTP keys. Therefore an understanding of OTP helps understand stream cipher techniques at all.

In OTP a plaintext is paired with a truly random secret key (a one-time pad). Then, each bit or character of the plaintext is encrypted by combining it with the corresponding bit or character from the pad using modular addition.

If you like, here is very simple visualization of OTP on youtube

However, practical problems have prevented OTPs from being widely used. In particular are these requirements:

• OTP needs to be minimum as long as the message
• OTP should be completely random (not pseudo-random)
• OTP cannot be reused.

Initialization Vector

Unfortunately, common hardware in computers can only generate pseudorandom vectors. The pseudorandom keystream is typically generated serially from a random seed value using pseudorandom number generator (PRNG)². That could be a software or hardware module and is able to create endless Keystream that will be identical on both sides. It will be identical of course only if the same register design and same Seed Sequence called Initialization vector (IV) (sometimes Starting Variable (SV)) is used on both sides.

It’s practical to use the determinism of PRNGs to generate the same Keystreams. But that means IV needs to be chosen carefully, always randomly, and cannot be repeated.

To produce Secret Keystream IV will be combined with Secret Key and the Secret Key is never exchanged insecurely. But IV is normally exchanged not encrypted, even more with some Modes of operation it is forbidden to encrypt IV because it weakens security.

An IV is essential when the same key might ever be used to encrypt more than one message. An IV basically mixes some unique, non-secret data into the key to prevent the same key from ever being used twice. A weak IV is part of what made WEP breakable.

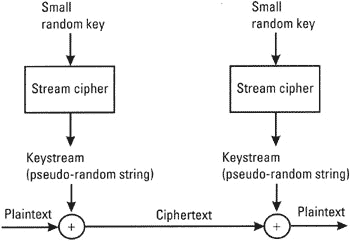“Small random key” acts as IV for PRNG

Stream cipher Synchronization

If sender and receiver generate Keystream independently of each other for a long time, the probability that something gets out of synch rises. Consider a bit is swapped on the line…

Synchronous stream cipher

If a stream of pseudo-random digits is generated independently of the plaintext and ciphertext messages such chipper is referred to as synchronous stream cipher. In a synchronous stream cipher, the sender and receiver must be exactly in step for decryption to be successful. However, synchronization can get lost. To restore synchronization, various offsets can be tried systematically to obtain the correct decryption. Another approach is to tag the ciphertext with markers at regular points in the output.

Self-synchronizing stream ciphers

Another approach uses several of the previous N ciphertext digits to compute the keystream. Such schemes are known as self-synchronizing stream ciphers, asynchronous stream ciphers, or ciphertext autokey (CTAK). The receiver will automatically synchronize with the keystream generator after receiving N ciphertext digits, making it easier to recover if digits are dropped or added to the message stream.

Stream cipher haracteristic

Stream ciphers typically execute at a higher speed than block ciphers and require lower hardware complexity (and memory usage).

Popular stream ciphers

• RC4 - (meanwhile considered insecure!)
• Salsa20
• SEAL
• A5/1,A5/2 - are used in GSM and ==considered weak and insecure!==
• SNOW 3G - synchronous stream cipher
• HC-256 - gains popularity
• Rabbit - gains popularity
• SEAL - one of the fastest stream ciphers
• Salsa20 - very efficient and secure. ChaCha variant was selected as a replacement for RC4 in OpenSSL.

Block cipher

The main difference to stream ciphers is that block ciphers operate on large blocks of digits with a fixed, unvarying transformation.

The modern design of block ciphers is based on the concept of an iterated product cipher³. The product cipher combines a sequence of simple transformations such as substitution (s-box), permutation (p-box), and modular arithmetic. I will not go into details here.

Mode of Operation

Since a block cipher by itself can only encrypt/decrypt of one fixed-length group of bits called a block additional techniques needed to encrypt Messages that are longer than a single block size. Therefore a mode of operation describes how to repeatedly apply a cipher’s single-block operation to securely transform amounts of data larger than a block.

Electronic Codebook (ECB)

ECB is the simplest of the operation modes. The message is divided into blocks, and each block is encrypted separately with the same key. 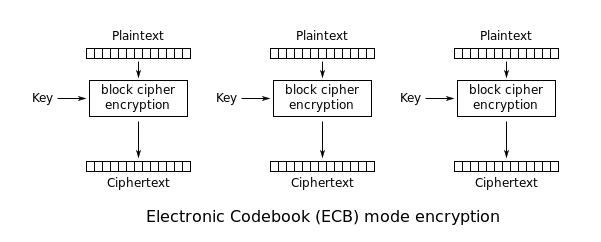==The huge disadvantage of this method is that identical plaintext blocks are encrypted into identical ciphertext blocks==. To illustrate the problem let’s consider an image file that is encrypted with some block-cipher in ECB mode.

Anyway, this mode has advantages: Encryption, decryption and random block access are parallelizable.

Cipher Block Chaining (CBC)

CBC was designed to eliminate the pattern attack problem of ECB

In CBC mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, an IV must be used in the first block. CBC has been the most commonly used mode of operation. Its main drawback is that encryption is sequential (cannot be parallelized).

For example, CBC mode is the default mode of operation for OpenVPN.

Propagating Cipher Block Chaining (PCBC)

In PCBC mode, each block of plaintext is XORed with the XOR of the previous plaintext block and the previous ciphertext block before being encrypted. No parallelized operation is possible. PCBC is not widely used.

Cipher Feedback (CFB)

CFB decryption is almost identical to CBC encryption performed in reverse. Also, CFB mode makes a block cipher into a self-synchronizing stream cipher.

Output Feedback (OFB)

OFB mode makes a block cipher into a synchronous stream cipher as well. It generates keystream blocks, which are then XORed with the plaintext blocks to get the ciphertext. No parallelism is possible. OFB means encrypting the IV again and again to produce the keystream. If you end up in a cycle, the keystream will start repeating itself. (This should not be a practical weakness, but why chance it?)

Counter (CTR)

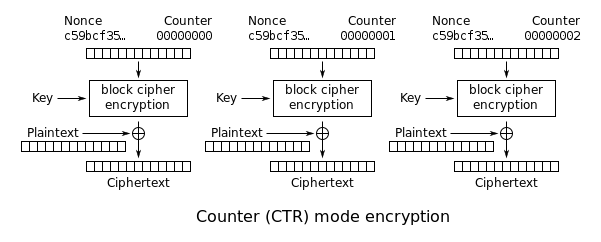
Like OFB, block cipher with CTR can be seen as a kind of stream cipher. Here Keystream is generated blockwise by encrypting successive values of a counter. Here counter can be any function that produces a sequence that is guaranteed not to repeat for a long time, although an actual increment-by-one counter is the simplest and most popular. Today CTR mode is widely accepted, along with CBC, CTR mode is one of two block cipher modes most recommended. CTR mode is well suited to operate on a multi-processor machine where blocks can be encrypted and decrypted in parallel. Furthermore, it does not suffer from the short-cycle problem that can affect OFB.

Padding

We learned about the Mode of Operation only last thing is left to mention left and that is padding. Block cipher modes for symmetric-key encryption algorithms require plain text input that is a multiple of the block size, so messages may have to be padded to bring them to this length. But if you encrypt using CFB or OFB or CTR modes then the ciphertext will be the same size as the plaintext and so padding is not required. But is important for ECB, CBC, and PCBC.

I will mention only a few examples below.

Bit padding

According to ISO/IEC 9797-1 as Padding Method 2.

1011 1001 1101 0100 0010 011 - 1 0000 0000 

ANSI X.923

In ANSI X.923 bytes filled with zeros are padded and the last byte defines the padding boundaries or the number of padded bytes.

| DD DD DD DD DD DD DD DD | DD DD DD DD - 00 00 00 04 |

PKCS7

Padding is in whole bytes. The value of each added byte is the number of bytes that are added, i.e. N bytes, each of value N is added. The number of bytes added will depend on the block boundary to which the message needs to be extended.

| DD DD DD DD DD DD DD DD | DD DD DD DD DD DD - 02 02 |
| DD DD DD DD DD DD DD DD | DD DD DD DD DD - 03 03 03 |
| DD DD DD DD DD DD DD DD | DD DD DD DD - 04 04 04 04 |

PKCS#5 padding is identical to PKCS#7 padding, except that it has only been defined for block ciphers that use a 64-bit (8 bytes) block size.

Now we know that block ciphers can be described by the cipher + mode of operation + padding. Some ciphers have several variants or need additional parameters like key length to be distinct described. ###Popular block ciphers Finally here is the outline of the most popular block ciphers

DES

The Data Encryption Standard (DES)* developed in the early 1970s at IBM and based on an earlier design by Horst Feistel. DES was published as FIPS Standard for the US in 1977 and lasted until October 2000. DES is now considered to be insecure for many applications. This is mainly due to the 56-bit key size being too small. Some documentation makes a distinction between DES as a standard and DES as an algorithm, referring to the algorithm as the DEA (Data Encryption Algorithm).

AES

The Advanced Encryption Standard (AES), also known as Rijndael(its original name), is a specification for the encryption of electronic data by the U.S. NIST in 2001. For AES, NIST selected three members of the family, each with a block size of 128 bits, but three different key lengths: 128, 192, and 256 bits. AES is the first (and only) publicly accessible cipher approved by the National Security Agency (NSA) for top secret information when used in an NSA-approved cryptographic module.

Intel processors since Westmere in 2010 come with AES hardware support[^4] that makes AES operations effectively free.

Other block ciphers

• IDEA (1990, International Data Encryption Algorithm): Used in PGP
• Blowfish 1993. Autor Bruce Schneier
• Twofish (used by Microsoft)
• CAST-128, CAST-256: Block ciphers from Carlisle M. Adams
• Serpent: Block ciphers from Ross Anderson, Eli Biham and Lars Knudsen,
• RC5

Block Cipher Learning

We’ve learned that with the Cipher kind DES, AES or whatever Mode of Operation need to be chosen. With some modes of Operation Padding needs to be chosen and good Initialization Vector as well.

To consolidate that learning i’ve prepared several Java expamples

Java Examples

Encrypt Message with AES in ECB mode with PKCS5Padding

byte[] encryptText = originalText.getBytes();
SecretKey skeySpec = new SecretKeySpec(secretKey, "AES");
Cipher cipher = Cipher.getInstance("AES/ECB/PKCS5Padding");
cipher.init(Cipher.ENCRYPT_MODE, skeySpec);
encrypted = cipher.doFinal(encryptText);

As you see only secretKey and plaintext is needed here. But we’ve learned that other Mode of operation need also IV. So let’s look at CBC Example. Here iv is additional new paramater.

byte[] encryptText = originalText.getBytes();
SecretKey skeySpec = new SecretKeySpec(secretKey, "AES");
Cipher cipher = Cipher.getInstance("AES/CBC/PKCS5Padding"); 
IvParameterSpec ivspec = new IvParameterSpec(iv);
cipher.init(Cipher.ENCRYPT_MODE, skeySpec, ivspec);
encrypted = cipher.doFinal(encryptText);

For CTR mode i would look similar but no padding is needed, so instead of AES/CBC/PKCS5Padding``you can just use AES/CTR/NoPadding` You will find the whole example on Github There you’ll find how IV and Keys are generated.

Disclaimer

Cryptography needs an extra level of precision. So please comment or give me a hint if something is not precise as it should be. Please double-check the difficult moment, before you implement cryptography.

[^4:] AES instruction set. Some performance analysis showed an increase in throughput from approximately 28.0 cycles per byte to 3.5 cycles per byte with AES/GCM versus a Pentium 4 with no acceleration.